Learning how do you find the z score is essential for anyone working with statistical data analysis. The Z score, also known as the standard score, is a key concept in statistics that tells you how far a particular value is from the average, measured in units called standard deviations. This powerful statistical tool helps compare data points from different sets and understanding where a value stands on a scale. When you master how do you find the z score, you unlock the ability to make informed decisions in trading, finance, and statistical analysis. Z scores are essential in many areas, especially when you want to test hypotheses or evaluate performance metrics in financial markets.
For example, if you score higher than most students on a test, your Z score will show just how much better you performed compared to the average. This score is widely used in fields like standardized testing, finance for measuring stock returns, and quality control in manufacturing. Understanding how do you find the z score is particularly valuable for traders analyzing market volatility and risk assessment.
Visualizing the Z score on a standard normal curve—a bell-shaped graph—helps us quickly see how common or rare a value is compared to the rest. Understanding Z scores lays the foundation for more detailed analysis, calculations, and interpretations covered in the next sections.
Real-world uses include:
- Assessing student performance relative to peers
- Evaluating financial risk and returns in trading strategies
- Monitoring product quality against standards
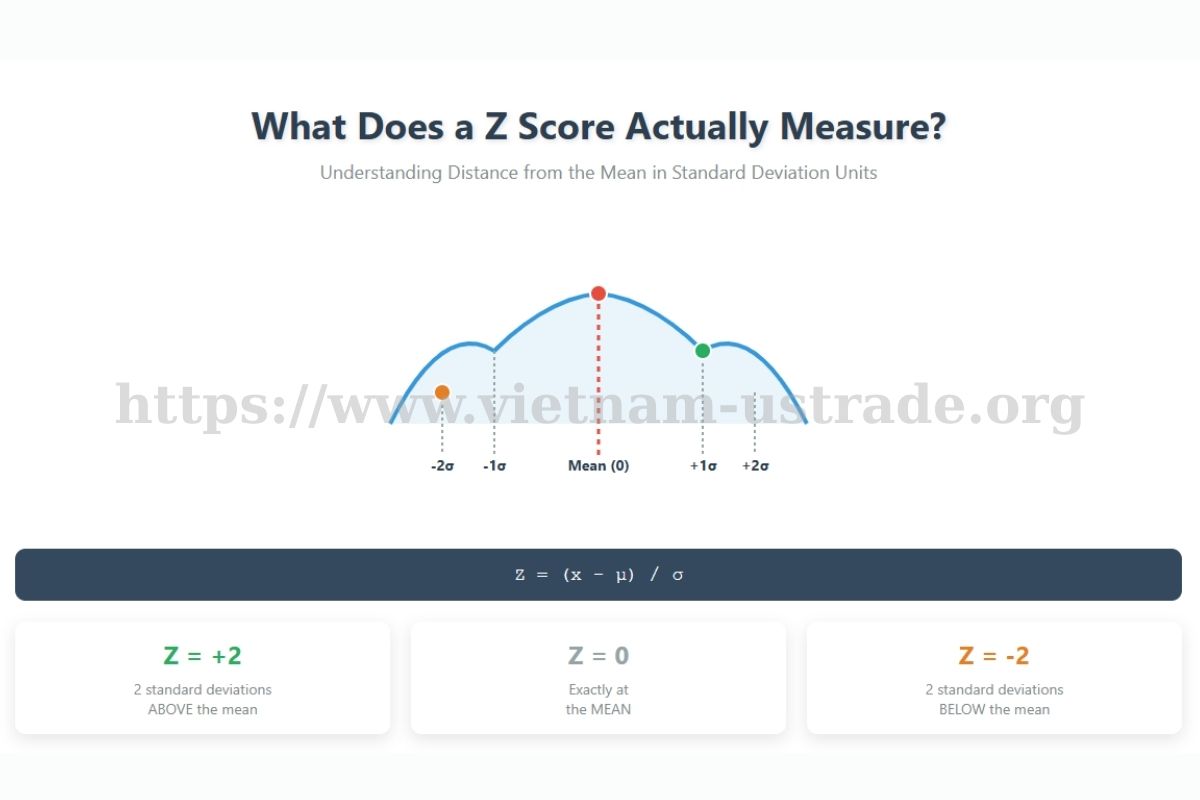
1. What Does a Z Score Actually Measure?
When exploring how do you find the z score, it’s crucial to understand what this metric actually measures. A Z score measures how far a specific value is from the mean (average). It shows whether the value is above, below, or exactly at the average. The number itself is in standard deviation units, making it easy to understand distances on the data scale.
A positive Z score means the value is above the mean, while a negative score means it’s below. A Z score of zero means the value is right on the average.
Why is this useful? It helps identify unusual or rare values, called outliers. For example, a Z score of +3 means the value is three standard deviations above the average, likely meaning it’s rare or exceptional. This concept is particularly relevant when analyzing options trading scenarios where understanding probability distributions is crucial.
Fields making key use of Z scores include:
- Psychology, to understand test results
- Education, to rank student scores
- Business analytics, to spot trends or anomalies
Example: If a student has a Z score of +2 in math, they scored two standard deviations above the average, indicating strong performance.
2. How Do You Find the Z Score? The Formula and Core Concept
Formula: z = (x - μ) / σ
Understanding how do you find the z score starts with mastering this fundamental formula. Here’s what each term means:
- x: The value you want to evaluate
- μ (mean): The average of all data points
- σ (standard deviation): The typical distance of data points from the mean
This formula standardizes your value, adjusting for different averages and spreads across datasets. By converting values into Z scores, you can compare data from different groups or understand how typical or extreme a value is. This standardization process is similar to how traders use normalized indicators to compare different financial instruments.
For example, if the average test score is 70, the standard deviation is 10, and your score is 85, then your Z score is (85 – 70) / 10 = 1.5. This means your score is 1.5 standard deviations above the average.
3. Step-By-Step: How Do You Find the Z Score For Any Data?
Follow these simple steps to calculate a Z score for any data point:
- Find the mean (μ) of your dataset. Add all values and divide by the number of values.
- Calculate the standard deviation (σ). This measures how spread out the values are around the mean.
- Select your value (x). This is the data point you want to find the Z score for.
- Plug your values into the formula: z = (x – μ) / σ.
- Calculate the result and interpret it.
Here is a table to illustrate the steps with examples:
| Step | Example 1 (Above Mean) | Example 2 (Below Mean) |
|---|---|---|
| Mean (μ) | 50 | 50 |
| Standard Deviation (σ) | 5 | 5 |
| Value (x) | 60 | 40 |
| Calculate Z score | (60 – 50)/5 = 2 | (40 – 50)/5 = -2 |
| Interpretation | Value is 2 SDs above mean | Value is 2 SDs below mean |
By working through these steps, anyone can find the Z score and understand its meaning within any dataset.
Quick definitions:
- Mean: Average value in a dataset
- Standard Deviation: Measure of how values spread out
4. Common Scenarios and Use Cases for Finding the Z Score
Z scores come up in many fields, including financial markets where understanding statistical distributions is crucial for risk management. Let’s compare a few common uses:
| Field | Dataset | Mean (μ) | SD (σ) | Value (x) | Z Score | Interpretation |
|---|---|---|---|---|---|---|
| Education | Test Scores | 75 | 8 | 90 | 1.88 | Well above average score |
| Finance | Stock Returns % | 0.5 | 2 | -3 | -1.75 | Lower than average return, possible loss |
| Healthcare | Blood Pressure | 120 | 15 | 150 | 2.00 | Higher than normal pressure |
These examples show how Z scores help professionals quickly spot values that differ from the average, be it a student’s achievement, market performance, or patient data. In trading, this statistical approach is similar to identifying overbought or oversold conditions using technical indicators.
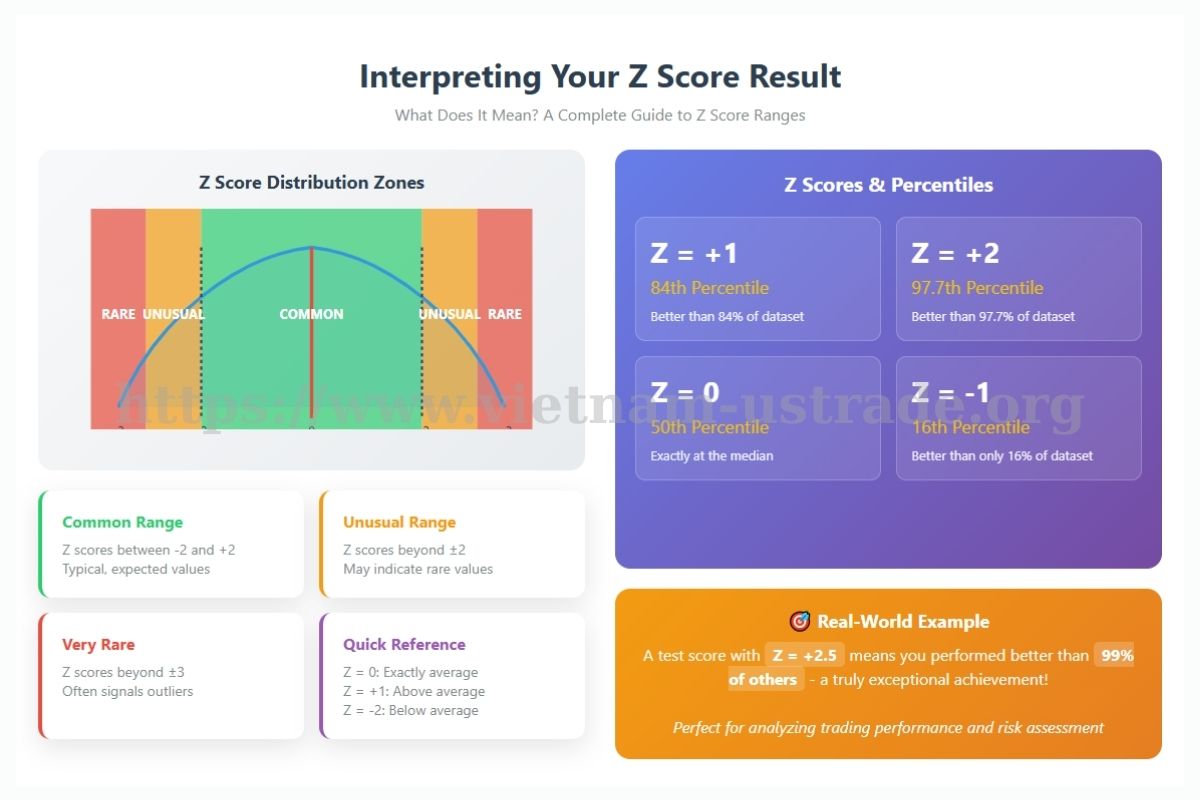
5. Interpreting Your Z Score Result: What Does It Mean?
Understanding the meaning of your Z score is as important as calculating it. Generally:
- A Z score between -2 and +2 is considered common or typical.
- Z scores beyond ±2 may indicate unusual or rare values.
- Z scores beyond ±3 are very rare, often signaling outliers.
Z scores can also be related to percentiles using tables or online calculators. For example, a Z score of +1 roughly corresponds to the 84th percentile, meaning the value is higher than 84% of the dataset. This percentile interpretation is particularly useful when analyzing futures and options probabilities.
Here’s a quick look at common interpretations:
- Z = 0: Exactly average
- Z = +1: Slightly above average
- Z = -2: Below average, possibly unusual
Imagine scoring a Z score of 2.5 on a test — this means you performed better than about 99% of others, a strong achievement.
For precise percentile matching, use an online percentile calculator.
6. Advanced How-Tos: Special Cases When Finding the Z Score
Sometimes, calculating Z scores isn’t straightforward. Here are some special situations to consider:
- Population vs. Sample: If you know the full population data, use the population mean and standard deviation. For samples, use sample statistics and adjust formulas accordingly.
- Unknown Population SD: If the population standard deviation is unknown, estimate it using the sample standard deviation. This introduces some uncertainty.
- Skewed or Non-Normal Data: Z scores assume data follows a normal distribution (bell curve). For skewed data, interpretation can be misleading.
- Small Samples: When dealing with few data points, consider t-scores instead of Z scores to account for extra variability.
These nuances help maintain accuracy when applying Z scores in complex or imperfect data situations, much like how traders must adjust their strategies based on market conditions and data quality.
7. Supplemental: FAQs for Finding a Z Score
- Can you find the Z score without knowing the population standard deviation? Yes, but you should use the sample standard deviation with caution. This is common in practical situations.
- Is the formula different for sample means? The formula is the same, but the standard deviation you use might come from the sample, which affects precision.
- What are common mistakes? Forgetting to subtract the mean or confusing the standard deviation with the variance are typical errors.
- When shouldn’t you use Z scores? Avoid using Z scores with data that is clearly not normally distributed or extremely small datasets without adjustment.
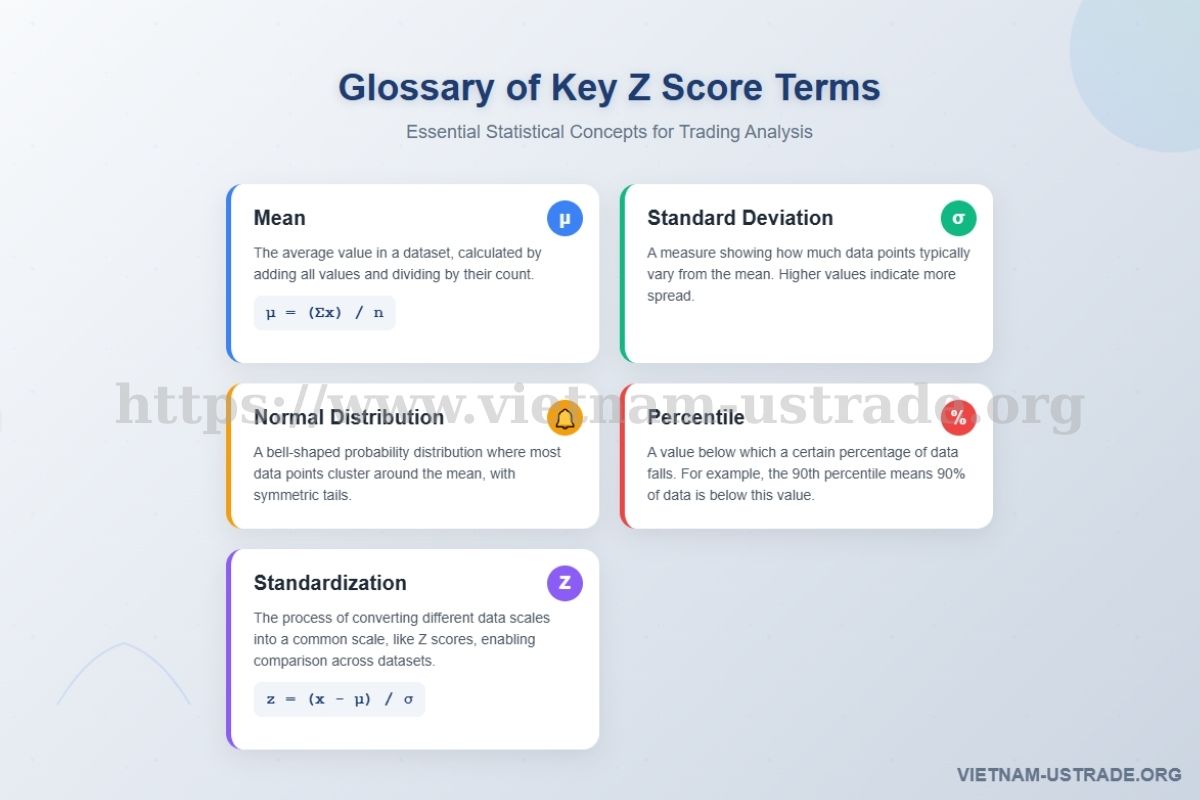
8. Glossary of Key Z Score Terms
- Mean: The average value in a dataset, calculated by adding all values and dividing by their count.
- Standard Deviation: A measure showing how much data points typically vary from the mean.
- Normal Distribution: A bell-shaped probability distribution where most data points cluster around the mean.
- Percentile: A value below which a certain percentage of data falls.
- Standardization: The process of converting different data scales into a common scale, like Z scores.
9. Conclusion
Mastering how do you find the z score is a powerful skill that provides easy-to-understand insights for comparing individual values with the overall dataset. Whether you are analyzing test results, financial data, or clinical measures, knowing how to calculate and interpret the Z score gives you valuable insights into how typical or rare a value is.
Understanding how do you find the z score becomes particularly valuable in trading and financial analysis, where statistical distributions help assess risk and probability. Remember that context matters—data distribution, sample size, and knowing when to use advanced methods will ensure your analysis is accurate and meaningful. When applying these statistical concepts to financial markets, consider exploring advanced trading techniques and risk management strategies.
Don’t forget to follow the Trader & Trading category on Vietnam-UStrade for the latest updates on statistical analysis in trading and comprehensive market insights. Use Z scores wisely to support clear, data-driven decisions across many fields, from academic research to professional trading strategies.
